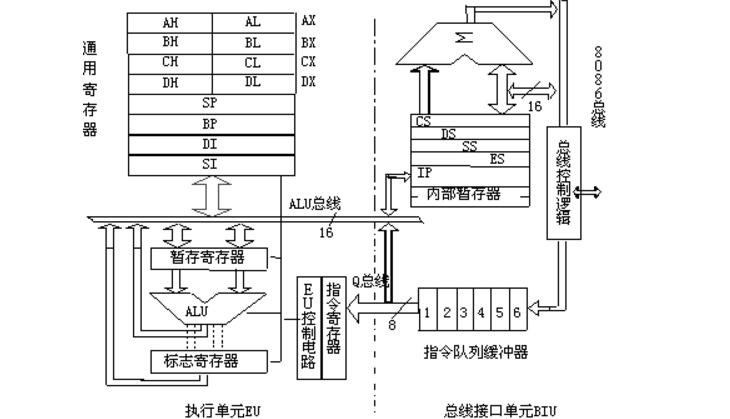
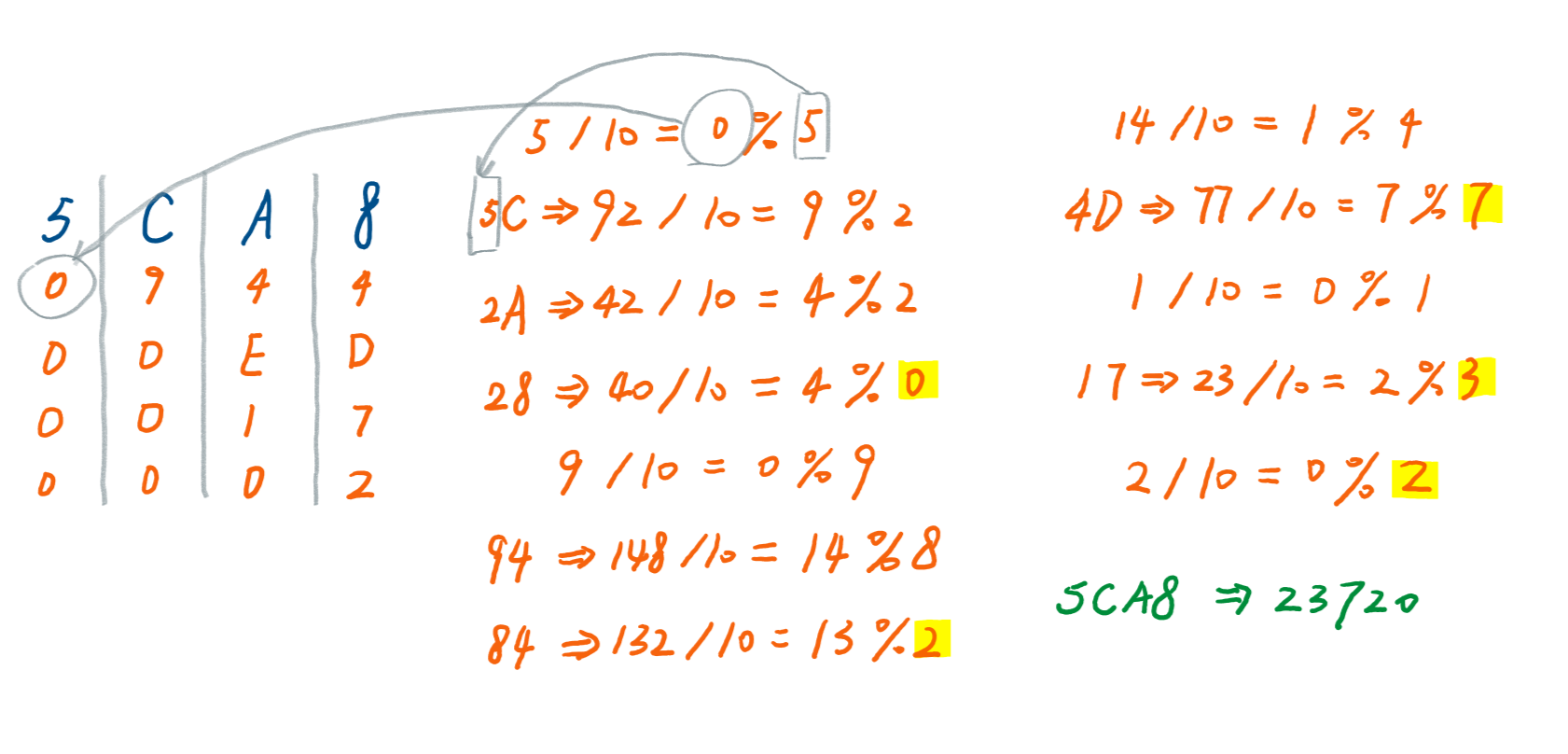8086汇编之64位长整数进制转换

近期正在学习8086汇编语言程序设计，这是学校里的一门专业选修课。首先上一张16位的8086CPU组成图：
8086CPU体系结构（字长16位）

作业中碰到这样一个问题：

在内存中存储一个64位的长整数，完成汇编程序在屏幕上显示其转换为10进制数后的结果。

由上图，所有的通用寄存器、段寄存器都只有16位，这意味着至少需要4个寄存器才能完整地存下该数；此外，8086指令集中的DIV指令最多支持32位÷16位的除法，因此也不能直接通过连除10来逐位获得转换为十进制的结果。

那么应当如何转换呢？苦苦思索大半天，最后在Stack Overflow上看到了一个十分巧妙的解法（原文）。

这个解法妙在充分利用了进制的数学含义，通过构造了一个递推式，从而能够实现通过简单的循环结构实现多寄存器之间的联动。假设待转换的数字从高到低分为N1:N2:N3:N4这四个同为16位的部分。那么如果我们将其看作一个四位的数，则有以下等式：

N1:N2:N3:N4 = N1 \times (2^{16})^3 + N2 \times (2^{16})^2 + N3 \times 2^{16} + N4 \tag{0}

代码中的核心步骤摘录如下：

                                ;here we have a 64bit number in si:di:cx:bx
loop0:  xor dx,dx
        mov ax,si               ;divide highes order by 10
        div diver
        mov si,ax
        mov ax,di               ;divide high order by 10
        div diver
        mov di,ax
        mov ax,cx               ;divide low oreder by 10
        div diver
        mov cx,ax
        mov ax,bx               ;divide lowest order by 10
        div diver
        mov bx,ax
                                ;right now we have the wanted number in dx
...

For DIV r/m16, DX:AX is divided by the given operand; the quotient is stored in AX and the remainder in DX.
对于DIV 寄存器/16位内存操作数形式的指令，DX:AX构成的数将除以操作数；商将被存在AX里，余数将被存在DX里。
———— 《Intel x86 Instruction Reference》

结合DIV指令的释义，这一段程序实际上做了下面这样的操作：

\begin{align} N1 &= N1' \times 10 + Rem1 \\ 2^{16} \times Rem1 + N2 &= N2' \times 10 + Rem2 \\ 2^{16} \times Rem2 + N3 &= N3' \times 10 + Rem3 \\ 2^{16} \times Rem3 + N4 &= N4' \times 10 + Rem4 \end{align}

原作者宣称，结束以上步骤之后，此时DX寄存器中的数即 $Rem4$ ，就是我们需要的十进制位数。每一次循环，都会从低到高产生一位数字，最后当所有N1-N4所有寄存器都为零时循环结束，产生的数字连接起来就是转换得到的十进制数。这个推论乍看上去十分令人迷惑，但是如果我们仔细观察上面的四个等式，马上就会有一个自然的想法：左右两边的RemX是否可以相互抵消掉？

我们令 $(1) \times 2^{16} + (2)$ ，可将 $Rem1$ 消除：

2^{16} \times N1 + N2 = 2^{16} \times 10 \times N1' + 10 \times N2' + Rem2 \tag{5}

接着，令 $(5) \times 2^{16} + (3)$ ，又可以消除Rem2. 以此类推，循环进行运算，我们最终可以得到这样一个式子：

N1 \times (2^{16})^3 + N2 \times (2^{16})^2 + N3 \times 2^{16} + N4 = 10 \times [N1' \times (2^{16})^3 + N2' \times (2^{16})^2 + N3' \times 2^{16} + N4'] + Rem4 \tag{6}

马上有两点重要的发现：

$(6)$ 式的左边恰好是 $(0)$ 式的右边，也就是说左边就是待转换的原数字；右侧是一个 $10 \times A + B$ 的形式，也就是说， $Rem4$ 正是原数字转换为十进制之后的个位数；
$(6)$ 式的右边，中括号内的部分其结构与左边原数字是相同的。也就是说，我们可以继续对这一部分做同样的处理，它将产生另一个" $Rem4'$ "，根据数制的定义它就是原数字转换后的十位数！如此递归下去，我们将得到一个从低到高的数字序列，而这正是本题要求的答案。

至此，我们便从数学的形式证明了上述解法的正确性。事实上，这种方法并不局限于本题的情况：对于待转换数来讲，本题实际是将其看做了一个“ $2^{16}$ 进制”的数，那么无论待转换的数是什么进制，只要我们能按照 $(0)$ 中的方式将其分割为若干等长的小块，那么它就可以适用该方法；对于目标进制来讲就更加明显，只要更换上述方法中的除数，就可以转换为任意的进制。